6224 Agricultural Road
Phone: (604)-822-3860
Fax:(604)-822-5324

6224 Agricultural Road Phone: (604)-822-3860 Fax:(604)-822-5324 |
 |
My research is primarily
focused on
numerical relativity and relativistic hydrodynamics. The
goal of numerical relativity is to solve Einstein's
equations (EE)
numerically.
I am particularly interested in the physics of strongly gravitating
compact
objects and their interaction with surrounding matter. In many
astrophysical scenarios one can model matter as an ideal fluid.
Even with such an idealization the numerical simulation of
the system is very challenging. The use of advanced
numerical methods is required for most of the interesting calculations,
especially in 2D/3D. Therefore a significant fraction of my time is
devoted to the development of specialized software.
Adaptive mesh refinment and parallelization are the most important
paradigms used in the software development.
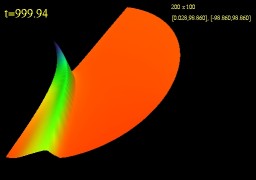 |
Numerical Relativistic hydrodynamics.
Many
astrophysical objects (stars, white dwarfs, neutron stars ) and various
phenomena observed in our Universe (accretion discs around black holes,
jets, ...) can be
(to various degree of accuracy) modeled by treating the constituting
matter as an ideal fluid. Therefore the ability to solve hydrodynamic
equations (Newtonian , relativistic or GR) in different
settings is crutial in providing better understanding of
the dynamics of these objects. The image to the left shows a
density of ideal fluid accreting onto Schwarzschild black hole. |
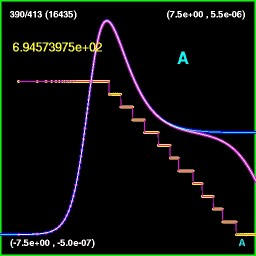
| Critical
phenomena in gravitational collapse. Critical phenomena
collectively refer to the behaviour observed at the threshold
of gravitational collapse; i.e. matter that is just on the verge of
forming a black hole. The most important properties include
universality and
self-similarity of the solution, and power law scaling relationships
for length scales emerging in near critical collapse. The image to the
right shows the continuously self similar solution of
critical collapse of ultrarelativistic fluid. |
 |
 |
Numerical
solution methods, high performance computing. One of the challenges
of developing code for the fully coupled Einstein-hydro system is
the necessity to merge different numerical techniques into a consistent
and efficient code. The hydrodynamic solver uses finite volume methods,
the field equations are solved with finite difference techniques and in
some cases elliptic equations must be also solved during the evolution
process (using multigrid). All this must be compatible with adaptive
mesh
refinement (AMR) and parallelizable. The image on the left shows an example of AMR hierarchical mesh structure. |
| Symbolic
algebra, general purpose computing on GPU(GPGPU). The equations we
encounter are in general complex and their translation into computer
code is a very error prone and time consuming process. A cleverly
designed program using some of the symbolic algebra software (Maple,
Mathematica) can greatly improve both of these aspects. The image on the right shows part of such Maple code. It has been known for some time that graphics processing units (GPU) are much more powerful in specialized floating point calculations than a general purpose processors (CPU). The gap in performance is expected to grow further as there is a huge commercial drive behind the GPU development (gaming industry). Today's GPUs are highly programable parallel units and I am interested in using their floating point power to accelerate numerical simulations. |
 |