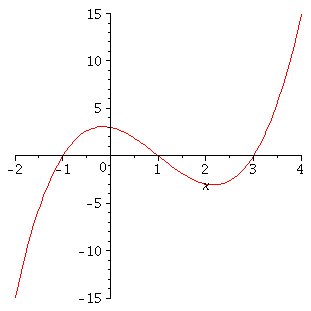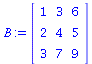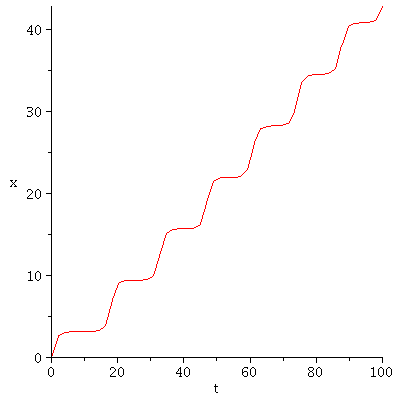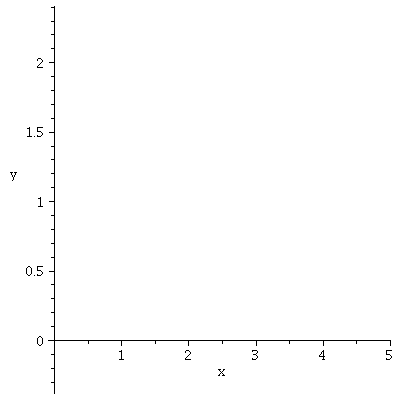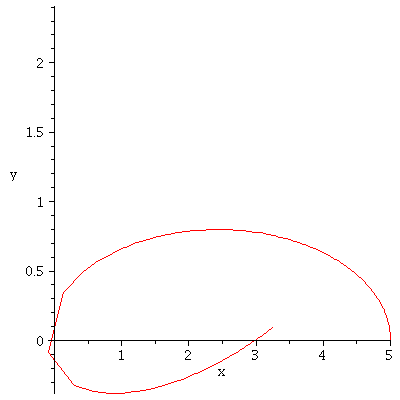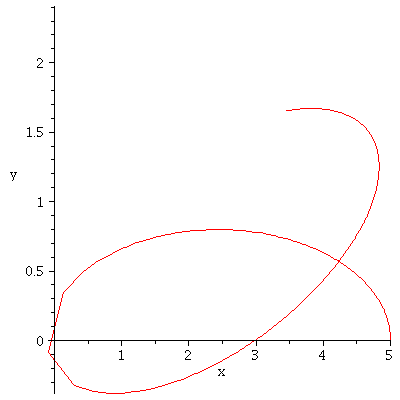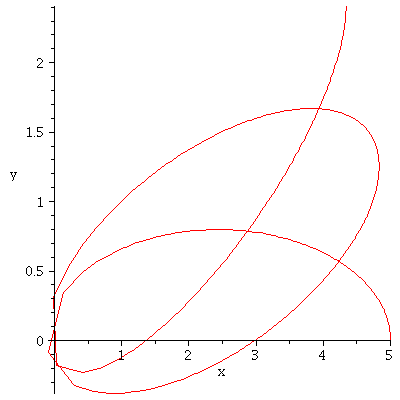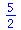 |
(1) |
 |
(2) |
 |
(3) |
 |
(4) |
 |
(5) |
 |
(6) |
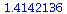 |
(7) |
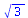 |
(8) |
 |
(9) |
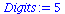 |
(10) |
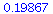 |
(11) |
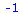 |
(12) |
 |
(13) |
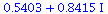 |
(14) |
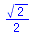 |
(15) |
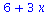 |
(16) |
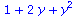 |
(17) |
| > |
factor(z^3+6*z^2+3*z-10); |
 |
(18) |
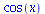 |
(19) |
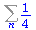 |
(20) |
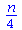 |
(21) |
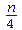 |
(22) |
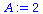 |
(23) |
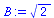 |
(24) |
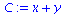 |
(25) |
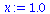 |
(26) |
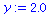 |
(27) |
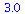 |
(28) |
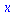 |
(29) |
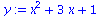 |
(30) |
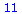 |
(31) |
| > |
z:=cos(x)^5+sin(x)^4+2*cos(x)^2-2*sin(x)^2-cos(2*x); |
 |
(32) |
 |
(33) |
| > |
f := x -> (x-1)*(x+1)*(x-3); |
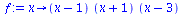 |
(34) |
 |
(35) |
 |
(36) |
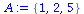 |
(37) |
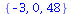 |
(38) |
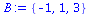 |
(39) |
 |
(40) |
 |
(41) |
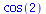 |
(42) |
| > |
G := {sin(x),cos(x),exp(x)}; |
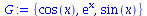 |
(43) |
 |
(44) |
![`:=`(A, array(1 .. 3, []))](maple_img/Intro_46.gif) |
(45) |
![`:=`(A[1], 0)](maple_img/Intro_47.gif) |
(46) |
![`:=`(A[2], `+`(`/`(`*`(Pi), `*`(3))))](maple_img/Intro_48.gif) |
(47) |
![`:=`(A[3], `+`(`/`(`*`(Pi), `*`(2))))](maple_img/Intro_49.gif) |
(48) |
](maple_img/Intro_50.gif) |
(49) |
| > |
B := array(1..3,1..3,[[1,3,6],[2,4,5],[3,7,9]]); |
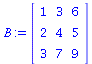 |
(50) |
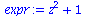 |
(51) |
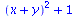 |
(52) |
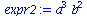 |
(53) |
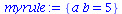 |
(54) |
| > |
simplify(expr2,myrule); |
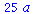 |
(55) |
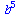 |
(56) |
| > |
solve({x^3-13*x+12},{x}); |
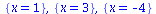 |
(57) |
| > |
solve({x+y=3,x-y=8},{x,y}); |
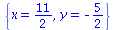 |
(58) |
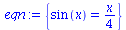 |
(59) |
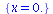 |
(60) |
| > |
fsolve(eqn,{x}, 0.01..2*Pi); |
 |
(61) |
| > |
f:= sin(x+y)-exp(x)*y = 0: |
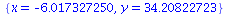 |
(62) |
| > |
fsolve({(x+1)^2=-2},x,complex); |
 |
(63) |
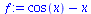 |
(64) |
 |
(65) |
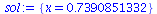 |
(66) |
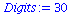 |
(67) |
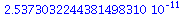 |
(68) |
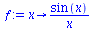 |
(69) |
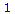 |
(70) |
| > |
limit(tan(x),x=Pi/2,left); |
 |
(71) |
| > |
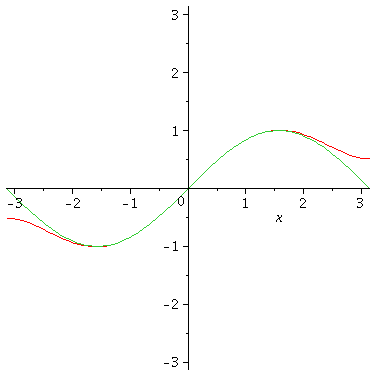
P:= series(sin(x),x=0); |
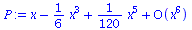 |
(72) |
| > |
P2 := convert(P,polynom); |
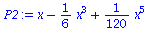 |
(73) |
| > |
plot({P2,sin(x)},x=-Pi..Pi,-Pi..Pi); |
| > |
ode1 := diff(y(t),t,t) = -g - k*diff(y(t),t); |
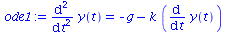 |
(74) |
| > |
ode2 := diff(x(t),t,t) = -k*diff(x(t),t); |
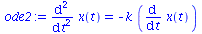 |
(75) |
| > |
ics1 := y(0)=0,D(y)(0)=vy; |
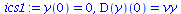 |
(76) |
| > |
ics2 := x(0)=0,D(x)(0)=vx; |
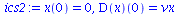 |
(77) |
| > |
sol1:=dsolve({ode1,ics1}); |
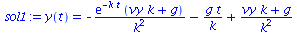 |
(78) |
| > |
sol2:=dsolve({ode2,ics2}); |
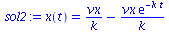 |
(79) |
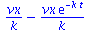 |
(80) |
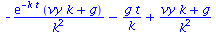 |
(81) |
| > |
vx:=1.0:vy:=1.0:g:=9.8: |
| > |
animate(plot,[[x(t),y(t),t=0..0.2]],k=0..10,trace=10,frames=100); |
| > |
 |
 |
(83) |
| > |
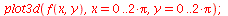 |
| > |
 |
| > |
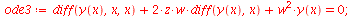 |
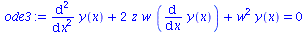 |
(84) |
| > |
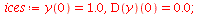 |
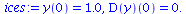 |
(85) |
| > |
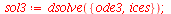 |
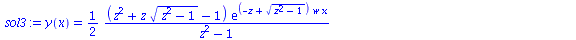
 |
(86) |
| > |
 |
| > |
 |
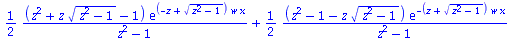 |
(87) |
| > |
 |
 |
(88) |
| > |
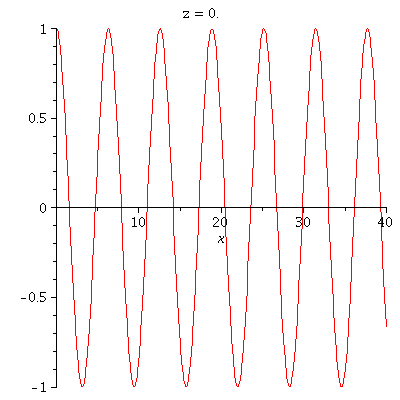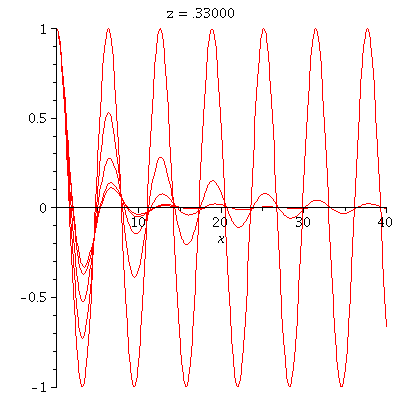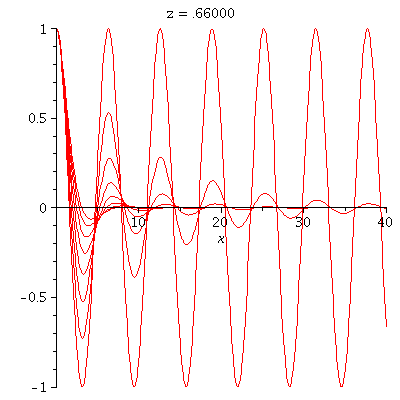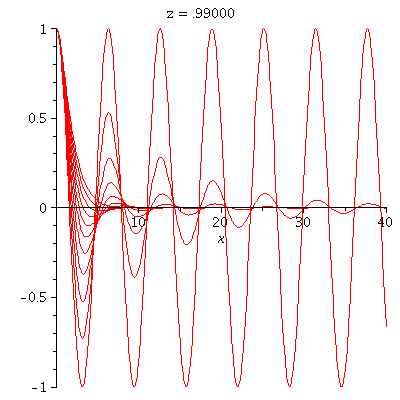
![animate(plot, [y(x), x = 0 .. 40], z = 0 .. .99, trace = 10, frames = 100); 1](maple_img/Intro_110.gif) |
| > |
 |
| > |
 |
 |
(89) |
| > |
 |
 |
(90) |
| > |
 |
 |
(91) |
| > |
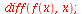 |
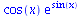 |
(92) |
| > |
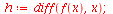 |
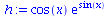 |
(93) |
| > |
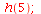 |
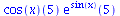 |
(94) |
| > |
 |
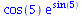 |
(95) |
| > |
 |
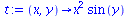 |
(96) |
| > |
); 1](maple_img/Intro_129.gif) |
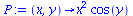 |
(97) |
| > |
); 1](maple_img/Intro_131.gif) |
 |
(98) |
| > |
); 1](maple_img/Intro_133.gif) |
](maple_img/Intro_134.gif) |
(99) |
| > |
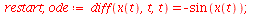 |
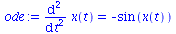 |
(100) |
| > |
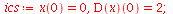 |
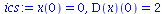 |
(101) |
| > |
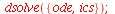 |
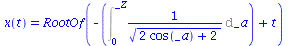 |
(102) |
| > |
 |
 |
(103) |
| > |
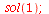 |
![[t = 1., x(t) = 1.73153917235197929, diff(x(t), t) = 1.29610910343914920]](maple_img/Intro_144.gif) |
(104) |
| > |
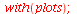 |
| > |
![odeplot(sol, [t, x(t)], 0 .. 100); 1](maple_img/Intro_154.gif) |
| > |
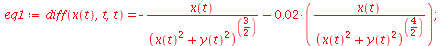 |
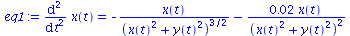 |
(106) |
| > |
 |
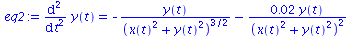 |
(107) |
| > |
 |
 |
(108) |
| > |
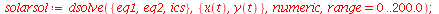 |
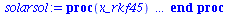 |
(109) |
| > |
 |
![[t = 0., x(t) = 5., diff(x(t), t) = 0., y(t) = 0., diff(y(t), t) = .100000000000000]](maple_img/Intro_165.gif) |
(110) |
| > |
![odeplot(solarsol, [x(t), y(t)], 0 .. 50.00, frames = 300); 1](maple_img/Intro_166.gif) |
last update: Wed May 11, 2016